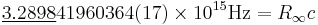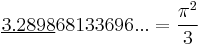Mathematical coincidence
A mathematical coincidence can be said to occur when two expressions show a near-equality that lacks direct theoretical explanation. For example, there's a near-equality around the round number 1000 between powers of two and powers of ten: 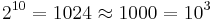 . Some of these coincidences are used in engineering when one expression is taken as an approximation of the other.
. Some of these coincidences are used in engineering when one expression is taken as an approximation of the other.
Contents |
Introduction
A mathematical coincidence often involves an integer, and the surprising (or "coincidental") feature is the fact that a real number arising in some context is considered by some ill-defined standard as a "close" approximation to a small integer or to a multiple or power of ten, or more generally, to a rational number with a small denominator.
Given the countably infinite number of ways of forming mathematical expressions using a finite number of symbols, the number of symbols used and the precision of approximate equality might be the most obvious way to assess mathematical coincidences; but there is no standard, and the strong law of small numbers is the sort of thing one has to appeal to with no formal opposing mathematical guidance. Beyond this, some sense of mathematical aesthetics could be invoked to adjudicate the value of a mathematical coincidence, and there are in fact exceptional cases of true mathematical significance (see Ramanujan's constant below, which made it into print some years ago as a scientific April Fools' joke[1]). All in all, though, they are generally to be considered for their curiosity value or, perhaps, to encourage new mathematical learners at an elementary level.
Some examples
Rational approximants
Sometimes simple rational approximations are exceptionally close to interesting irrational values. These are explainable in terms of large terms in the continued fraction representation of the irrational value, but further insight into why such improbably large terms occur is often not available.
Rational approximants (convergents of continued fractions) to ratios of logs of different numbers are often invoked as well, making coincidences between the powers of those numbers.[2]
Many other coincidences are combinations of numbers that put them into the form that such rational approximants provide close relationships.
Concerning pi
- The first convergent of π, [3; 7] = 22/7 = 3.1428..., was known to Archimedes,[3] and is correct to about 0.04%. The third convergent of π, [3; 7, 15, 1] = 355/113 = 3.1415929..., found by Zu Chongzhi,[4] is correct to six decimal places;[3] this high accuracy comes about because π has an unusually large next term in its continued fraction representation: π = [3; 7, 15, 1, 292, ...].[5]
- A coincidence involving π and the golden ratio φ is given by
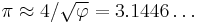 . This is related to Kepler triangles.
. This is related to Kepler triangles.
- The Feynman point is a sequence of six 9s that begins at the 762nd decimal place of the decimal representation of pi. For a randomly chosen normal number, the probability of any chosen number sequence of six digits (including 6 of a number, 658020, or the like) occurring this early in the decimal representation is only 0.08%. Pi is conjectured, but not known, to be a normal number.
Concerning base 2
- The coincidence
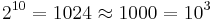 , correct to 2.4%, relates to the rational approximation
, correct to 2.4%, relates to the rational approximation 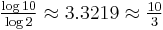 , or
, or 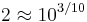 to within 0.3%. This relationship is used in engineering, for example to approximate a factor of two in power as 3 dB (actual is 3.0103 dB – see 3dB-point), or to relate a kilobyte to a kibibyte; see binary prefix.[6][7]
to within 0.3%. This relationship is used in engineering, for example to approximate a factor of two in power as 3 dB (actual is 3.0103 dB – see 3dB-point), or to relate a kilobyte to a kibibyte; see binary prefix.[6][7]
- This coincidence can also be expressed
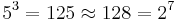 , and is invoked for instance in shutter speed settings on cameras, as approximations to powers of two in the sequence of speeds 125, 250, 500, etc.[2]
, and is invoked for instance in shutter speed settings on cameras, as approximations to powers of two in the sequence of speeds 125, 250, 500, etc.[2]
Concerning musical intervals
- The coincidence
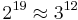 , from
, from 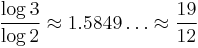 leads to the observation commonly used in music to relate the tuning of 7 semitones of equal temperament to a perfect fifth of just intonation:
leads to the observation commonly used in music to relate the tuning of 7 semitones of equal temperament to a perfect fifth of just intonation: 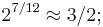 , correct to about 0.1%. The just fifth is the basis of Pythagorean tuning and most known systems of music. From the consequent approximation
, correct to about 0.1%. The just fifth is the basis of Pythagorean tuning and most known systems of music. From the consequent approximation 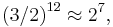 it follows that the circle of fifths terminates seven octaves higher than the origin.[2]
it follows that the circle of fifths terminates seven octaves higher than the origin.[2]
- The coincidence
![\sqrt[12]{2}\sqrt[7]{5} = 1.33333319\ldots \approx \frac43](/2012-wikipedia_en_all_nopic_01_2012/I/964ca2cc31e09cb0f3a386c48a7cd10c.png) leads to the rational version of 12-TET, as noted by Johann Kirnberger.
leads to the rational version of 12-TET, as noted by Johann Kirnberger.
- The coincidence
![\sqrt[8]{5}\sqrt[3]{35} = 4.00000559\ldots \approx 4](/2012-wikipedia_en_all_nopic_01_2012/I/0904eeced382e43fba48711a2afd003e.png) leads to the rational version of quarter-comma meantone temperament.
leads to the rational version of quarter-comma meantone temperament.
- The coincidence
![\sqrt[9]{0.6}\sqrt[28]{4.9} = 0.99999999754\ldots \approx 1](/2012-wikipedia_en_all_nopic_01_2012/I/00a2c2334554e524a0f2e83823d8dc43.png) leads to the very tiny interval of
leads to the very tiny interval of 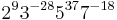 (about a millicent wide), which is the first 7-limit interval tempered out in 103169-TET.
(about a millicent wide), which is the first 7-limit interval tempered out in 103169-TET.
Numerical expressions
Concerning powers of pi
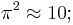 correct to about 1.3%.[8] This can be understood in terms of the formula for the zeta function
correct to about 1.3%.[8] This can be understood in terms of the formula for the zeta function 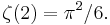 [9] This coincidence was used in the design of slide rules, where the "folded" scales are folded on
[9] This coincidence was used in the design of slide rules, where the "folded" scales are folded on  rather than
rather than 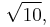 because it is a more useful number and has the effect of folding the scales in about the same place.
because it is a more useful number and has the effect of folding the scales in about the same place.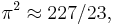 correct to 0.0004%.[8]
correct to 0.0004%.[8]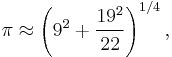 or
or 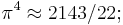 [10] accurate to 8 decimal places (due to Ramanujan: Quarterly Journal of Mathematics, XLV, 1914, pp350–372). Ramanujan states that this "curious approximation" to
[10] accurate to 8 decimal places (due to Ramanujan: Quarterly Journal of Mathematics, XLV, 1914, pp350–372). Ramanujan states that this "curious approximation" to  was "obtained empirically" and has no connection with the theory developed in the remainder of the paper.
was "obtained empirically" and has no connection with the theory developed in the remainder of the paper.
Some plausible relations hold to a high degree of accuracy, but are nevertheless coincidental. One example is:
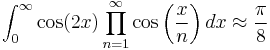
The two sides of this expression only differ after the 42nd decimal place.[11]
Containing both pi and e
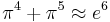 , within 0.000 005%[10]
, within 0.000 005%[10]
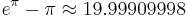 is very close to 20 (Conway, Sloane, Plouffe, 1988); this is equivalent to
is very close to 20 (Conway, Sloane, Plouffe, 1988); this is equivalent to 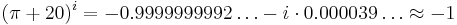 [10]
[10]
Containing pi or e and numbers 163 and 22
- Ramanujan's constant:
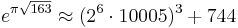 , within
, within 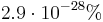 .[12] This fact is not a mathematical coincidence; it is a deep consequence of the fact that 163 is a Heegner number.
.[12] This fact is not a mathematical coincidence; it is a deep consequence of the fact that 163 is a Heegner number.
Other numerical curiosities
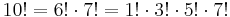 .[13]
.[13]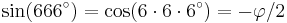 , where
, where  is the golden ratio[14] (an amusing equality with an angle expressed in degrees) (see Number of the Beast)
is the golden ratio[14] (an amusing equality with an angle expressed in degrees) (see Number of the Beast) , where
, where  is Euler's totient function[14]
is Euler's totient function[14]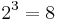 and
and 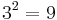 are the only non-trivial (i.e. at least square) consecutive powers of positive integers (Catalan's conjecture).
are the only non-trivial (i.e. at least square) consecutive powers of positive integers (Catalan's conjecture).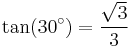 = 0.57735, very close to the Euler–Mascheroni constant.
= 0.57735, very close to the Euler–Mascheroni constant.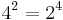 is the only positive integer solution of
is the only positive integer solution of 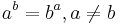 [15] (see Lambert's W function for a formal solution method)
[15] (see Lambert's W function for a formal solution method)- 31, 331, 3331 etc. up to 33333331 are all prime numbers, but then 333333331 is not.[16] See also Formula for primes.
- The Fibonacci number F296182 is (probably) a semiprime, since F296182 = F148091 × L148091 where F148091 (30949 digits) and the Lucas number L148091 (30950 digits) are simultaneously probable primes.[17]
- The solution to Fx=x+1, when multiplied by 200 is, to 4 decimal places is 1119.0000, almost exactly 1119.
- In a discussion of the birthday problem, the number
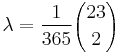 occurs, which is "amusingly" equal to
occurs, which is "amusingly" equal to 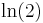 to 4 digits.[18]
to 4 digits.[18]
Decimal coincidences
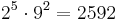 . This makes 2592 a nice Friedman number.[19]
. This makes 2592 a nice Friedman number.[19]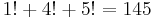 . The only such factorions (in base 10) are 1, 2, 145, 40585.[20]
. The only such factorions (in base 10) are 1, 2, 145, 40585.[20]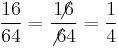 ,
, 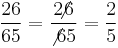 ,
, 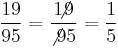 ,
, 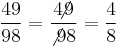 (anomalous cancellation[21])
(anomalous cancellation[21])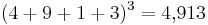 and
and 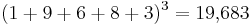 .[22]
.[22]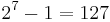 . This can also be written
. This can also be written 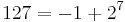 , making 127 the smallest nice Friedman number.[19]
, making 127 the smallest nice Friedman number.[19]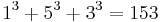 ;
; 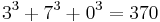 ;
; 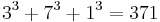 ;
; 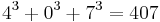 — all narcissistic numbers[23]
— all narcissistic numbers[23]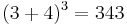 [24]
[24]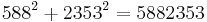 and also
and also 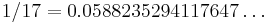 when rounded to 8 digits is 0.05882353. Mentioned by Gilbert Labelle in ~1980. 5882353 also happens to be prime.
when rounded to 8 digits is 0.05882353. Mentioned by Gilbert Labelle in ~1980. 5882353 also happens to be prime.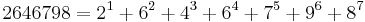 . The largest such number is 12157692622039623539.[25]
. The largest such number is 12157692622039623539.[25]- 73 is the 21st prime and 37 is the 12th prime. Both are reverse numbers. It is the only known combination.
Numerical coincidences in numbers from the physical world
Speed of light
The speed of light is exactly 299,792,458 m/s, very close to 300,000 km/s. This is a pure coincidence.[26]
Earth's diameter
The diameter of the Earth is almost exactly half a billion inches.[26] The metre was originally defined such that 40,000,000 m is within 0.02 percent of the earth's polar circumference.
Gravitational acceleration
While not constant but varying depending on latitude, the acceleration caused by Earth's gravity on the surface lies between 9.78 and 9.82 m/s2, which is quite close to 10. This means that as a result of Newton's second law, the weight of a kilogram of mass on Earth's surface corresponds roughly to 10 Newtons of force exerted on an object.
Rydberg constant
The Rydberg constant, when multiplied by the speed of light and expressed as a frequency, is close to 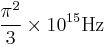 :[26]
:[26]
Avogadro Constant
The Avogadro constant is very nearly a power of 2.
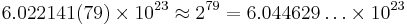
See also
- For a list of coincidences in physics, see anthropic principle
- Almost integer
- Birthday problem
- Exceptional isomorphism
- Narcissistic number
- Experimental mathematics
- Kepler triangle#A mathematical coincidence
References
- ^ Reprinted as Gardner, Martin (2001), "Six Sensational Discoveries", The Colossal Book of Mathematics, New York: W. W. Norton & Company, pp. 674–694, ISBN 0-393-02023-1.
- ^ a b c Manfred Robert Schroeder (2008). Number theory in science and communication (2nd ed.). Springer. pp. 26–28. ISBN 9783540852971. http://books.google.com/?id=2KV2rfP0yWEC&pg=PA27&dq=coincidence+circle-of-fifths+1024+7-octaves+%22one+part+in+a+thousand%22.
- ^ a b Petr Beckmann (1971). A History of Pi. Macmillan. pp. 101, 170. ISBN 9780312381851. http://books.google.com/?id=TB6jzz3ZDTEC&pg=PA101&dq=pi+113+355++digits.
- ^ Yoshio Mikami (1913). Development of Mathematics in China and Japan. B. G. Teubner. p. 135. http://books.google.com/?id=4e9LAAAAMAAJ&q=intitle:Development+intitle:%22China+and+Japan%22+355&dq=intitle:Development+intitle:%22China+and+Japan%22+355.
- ^ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics. CRC Press. p. 2232. ISBN 9781584883470. http://books.google.com/?id=_8TyhSqHUiEC&pg=PA2232&dq=pi+113+355++292+convergent.
- ^ Ottmar Beucher (2008). Matlab und Simulink. Pearson Education. p. 195. ISBN 9783827373403. http://books.google.com/?id=VgLCb7B3OtYC&pg=PA195&dq=3.0103+1024+1000.
- ^ K. Ayob (2008). Digital Filters in Hardware: A Practical Guide for Firmware Engineers. Trafford Publishing. p. 278. ISBN 9781425142469. http://books.google.com/?id=6nmnbIxpY3MC&pg=PA278&dq=3.0103-db.
- ^ a b Frank Rubin, The Contest Center – Pi.
- ^ Why is
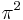 so close to 10?, Noam Elkies
so close to 10?, Noam Elkies - ^ a b c d e f g Weisstein, Eric W., "Almost Integer" from MathWorld.
- ^ http://crd.lbl.gov/~dhbailey/dhbpapers/math-future.pdf
- ^ Ramanujan, S. (1913/14). "Modular Equations and Approximations to pi". Quart. J. Pure Appl. Math. 45: 350–372.
- ^ Harvey Heinz, Narcissistic Numbers.
- ^ a b Weisstein, Eric W., "Beast Number" from MathWorld.
- ^ Ask Dr. Math, "Solving the Equation x^y = y^x".
- ^ Prime Curios!: 33333331 at The Prime Pages.
- ^ David Broadhurst, "Prime Curios!: 10660...49391 (61899-digits)".
- ^ Richard Arratia, Larry Goldstein, and Louis Gordon (1990). "Poisson approximation and the Chen-Stein method". Statistical Science 5 (4): 403–434. http://www.stat.wisc.edu/courses/st992-newton/smmb/files/align/arratia.pdf.
- ^ a b Erich Friedman, Problem of the Month (August 2000).
- ^ (sequence A014080 in OEIS)
- ^ Weisstein, Eric W., "Anomalous Cancellation" from MathWorld.
- ^ (sequence A061209 in OEIS)
- ^ (sequence A005188 in OEIS)
- ^ Prime Curios!: 343.
- ^ (sequence A032799 in OEIS)
- ^ a b c Michon, Gérard P.. "Numerical Coincidences in Man-Made Numbers". Mathematical Miracles. http://www.numericana.com/answer/miracles.htm. Retrieved 29 April 2011.
- ^ "Rydberg constant times c in Hz". Fundamental physical constants. NIST. http://physics.nist.gov/cgi-bin/cuu/Value?rydchz. Retrieved 25 July 2011.
External links
- (Russian) В. Левшин. – Магистр рассеянных наук. – Москва, Детская Литература 1970, 256 с.
- Hardy, G. H. – A Mathematician's Apology. – New York: Cambridge University Press, 1993, (ISBN 0-521-42706-1)
- Weisstein, Eric W., "Almost Integer" from MathWorld.
- Various mathematical coincidences in the "Science & Math" section of futilitycloset.com
- Press, W. H., Seemingly Remarkable Mathematical Coincidences Are Easy to Generate
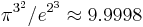
 ,
, 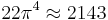 ,
, ![\sqrt[5]{\frac{163}{\log_e163}} \approx 2](/2012-wikipedia_en_all_nopic_01_2012/I/d5f599a33cb5d2b97800df8cda075f8d.png) ,
,